In case you don’t know it, Slitherlink is a puzzle in which you must divine the path of a line around a grid based only on numbers within that grid. The numbers tell you how many edges of their square are occupied by a segment of that line.
The only other rules are that there is one single line, which connects to itself, and cannot intersect itself at any point.
You can play some over at Brainbashers! Not sponsored!
I’ve quite levelled up my Slitherlink game in the past couple of weeks, and I’ve discovered a few principles that you can apply to resolve the next parts of the line. I’ll go in order of what I do when I start such a puzzle: the lowness of the hanging fruit.
0. Discipline!
This puzzle is far harder if you don’t put crosses on edges that cannot be part of the line. If nothing else, this is because some patterns of crosses imply the course of the line nearby, so not having them in place means you are working from half a songsheet.
One thing I find I have to remind myself often is that the numbers in the squares don’t just mean they can’t have more than that many lines; they also can’t have fewer. It’s easy to miss squares that have their maximum amount of crosses! Pay attention to those; if you ever fill in all the crosses a square can support, then you can fill in the line as well! Adding line segments then means you can try applying further rules.
Remember that you can consider the edge of the board as having another layer of squares, all edged with crosses, so whenever a rule mentions crosses, this works at the edge of the board as well.
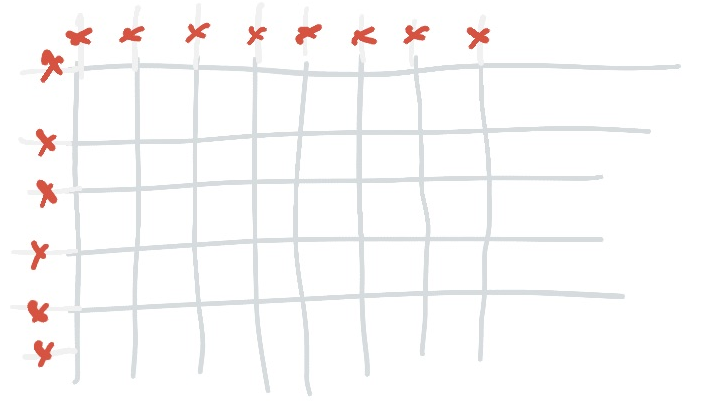
One last thing: loops. When you extend the line, check for edges that would make loops. This gets harder as you make the line longer, but you can often add a cross to the grid in order to prevent a loop. This usually helps you fill in near the edges, because the line is constrained there, so once it’s travelling somemwhere you often have to keep it away from itself!
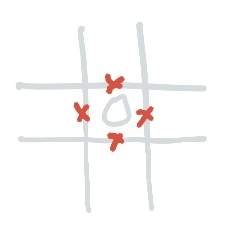
1. Zeroes
Zeroes are heroes because you can completely surround them with crosses. This might not sound so amazing, but the numbers nearby might now be forced to carry the line.
It’s super easy to go through the board and surround all your zeroes with crosses and then forget about them forever.
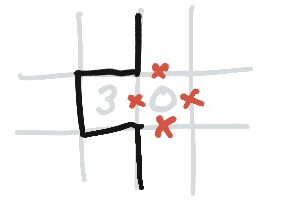
2. Threes
Threes are the next most constrained square. That’s because only one side is unique: the open side. Only one of its four sides may be a cross, which has a tendency to force the line to appear around threes.
Threes by Zeroes
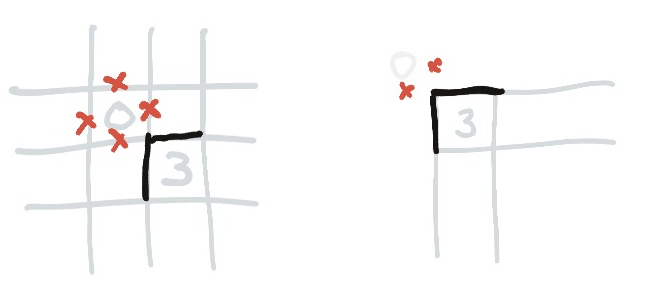
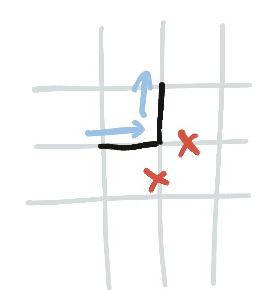
A three next to a zero has its cross side forced already. That means you can immediately fill in all three sides that have lines.
You can also extend the two edges where it meets the zero, because you’ve got two crosses in a corner and therefore you have to turn. I’ve put this as a separate rule, later, because you’re going to want to apply it on its own.
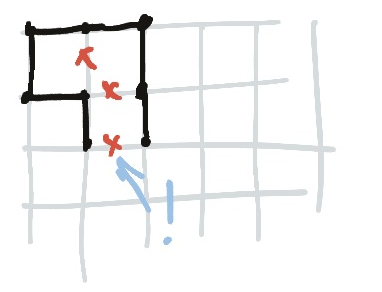
A three on the corner of a zero must use both of the edges that meet the zero.
Observe that at the corner of the board there is an imaginary zero, so any three in the corner of the board must have that corner filled in.
Threes by Threes
Orthogonally
A three next to a three must use the shared edge, and the edges opposite them. Additionally, the two edges that meet the shared edge straight-on must be crosses (but not the end edges!). This perpetuates, ladder-style, for as many threes as you have in a row.
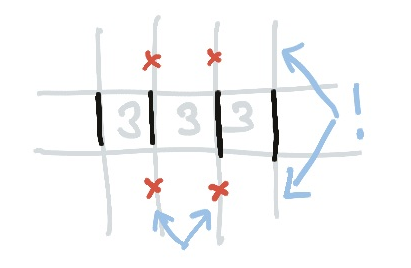
Later, when you learn about any of the missing edges, you can fill in the entire ladder because the filled edge and the empty edge will swap along the row. You can see why the first stage was possible: regardless of which way around they alternate, these edges will always be corners; but this was not true of the end ones, so you can put crosses there, now, too.
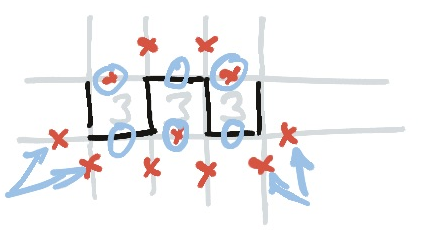
Additionally, you can fill in the opposite edge of any twos adjacent to the row of threes, and cross out the corners thereof! Probably better to just look at the picture for that one1.
Diagonally
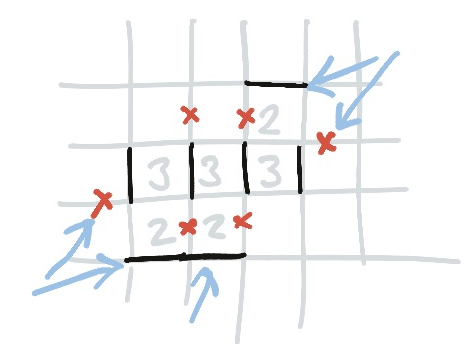
A three diagonally adjacent to another three must use the outside corners of the pair. This can sometimes give you a corner ladder on nearby twos.
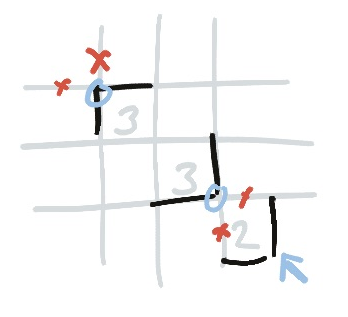
This is because there are only so many ways you can draw the curve around threes like this, and they all require those corners.
Because of the way twos interact with threes, this also works if there is any number of twos between them on this diagonal!
Approaching Threes
If your line approaches a three on any corner, the diagonally opposite corner of the three must be filled in. The opening of the three will be next to the vertex you approach it on.
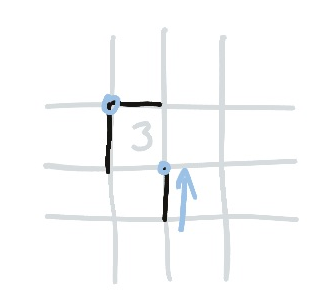
A related rule is that no vertex of a three can be a convex corner, because of the corner rules.
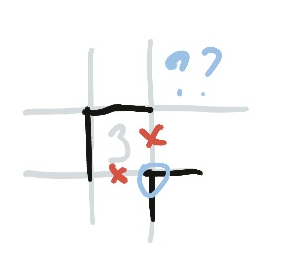
3. Twos
Corner Ladders
Similarly to the ladder of threes, you can make a ladder of twos if any of them commands a corner. Every two along that diagonal must use the same corner. You can see this, because if you apply the corner rule to the first corner you end up with two crosses on the next square; this being a two, it needs 2 line segments, which must be the other two. Repeat until your last diagonal two.
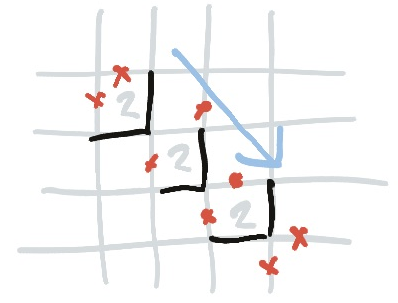
Twos and Threes
As a result of the corner rule applied to threes, if there is a two diagonally adjacent to a three you know that that two cannot use that corner. It can use one or neither of those edges, but not both.
This applies along the ladder, as well. The corresponding corner of the next two can also not be used, and so on and so forth.
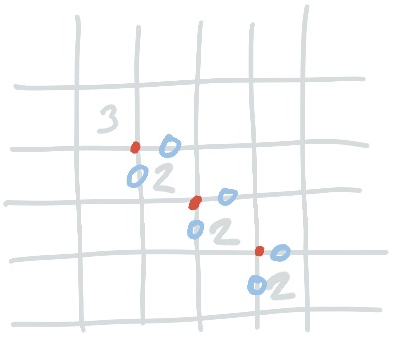
And there’s another trick! If you can eliminate a corner of any such ladder of twos, then by extension you can eliminate that corner of the three as well; this means one of those two edges must be the opening of the three, and thus the other two edges are line segments.
By the Edge
Twos by the edge (or by an equivalent set of crosses) must either use parallel edges including the edge of the board, or a sort of zig-zag shape where the line goes around the twos in corners. You can’t use parallel edges that go into the edge, because of dead ends.
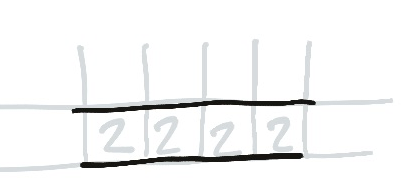
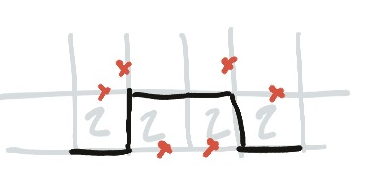
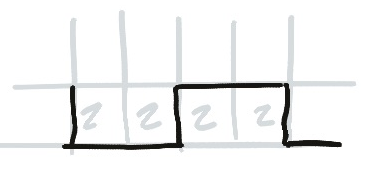
Remember that “the edge” and “a line of crosses” are equivalent, so you might end up with an “edge” in the middle of the board.
4. Ones
Ones by Crosses
Ones give you some information inasmuch as you know that you’re going to be making a lot of crosses when you complete one. This means that you can usually eliminate some edges of a one simply because if you used it, you would have to turn a corner and use another edge of the same square: not allowed!
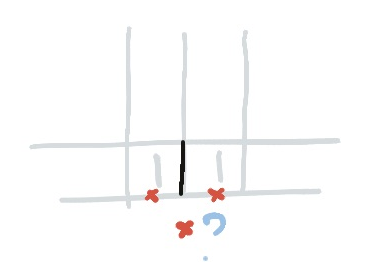
Remember there are imaginary crosses at the edge of the board. This means you can either go behind or in front of a row of ones at the edge, but never between them.
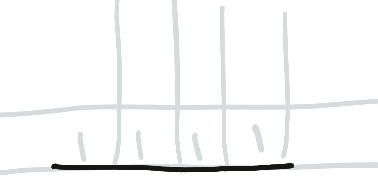
Ones by Zeroes
Not really adding much information, but of course if there is a one diagonally adjacent to a zero you can’t use either of the edges that meets the zero, because you have to use the other one to get out again!
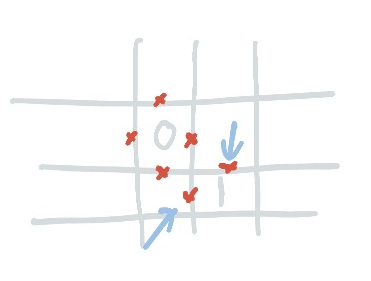
This applies anywhere you already have two crosses: a 1 makes two into four. You can apply this in reverse in situations where you only have two sides left of a 1: you can’t do anything that would cause this 4-cross cross to happen!
Approaching Ones
When the line approaches a one, the opposite edges must be eliminated. Note that this is only true if the line cannot turn away from the one. Don’t apply the rule too hastily.
5. Crosses
Crosses show where your line can’t go, and often therefore show where it must go.
It should be obvious (because I already mentioned it) that you can fill in the rest of the lines around a number when you’ve got enough crosses! You should try to do this immediately, because otherwise you’ll kick yourself for not realising when you’re struggling to find the next bit.
Creating corners
If a vertex has two crosses at right angles, then the line must form a right angle of the other two edges—or the line doesn’t use this vertex at all!
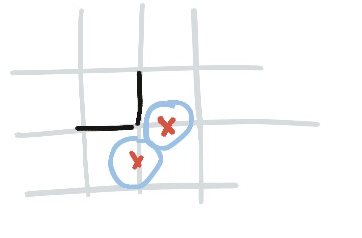
This is the reason you can make the Ω shape when you have a three next to a zero, and the reason you have to use both edges where a three is diagonally adjacent to a zero.
The opposite to this rule also holds true: if ever your line turns a right angle, then the other two edges at that vertex must be crosses. This is evident when you think about it: The line cannot meet itself, so if it turns a corner, that corner is off-limits!
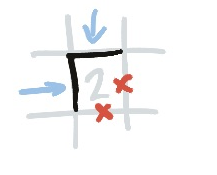
This is the reason you get a cascade of twos on the corners: Each one forces you to eliminate two edges of the next one, so the other two must be part of the line.
Dead Ends
If a vertex on the board has three crosses around it, the fourth line must also be a cross! That’s because if you fill it in with a line, where will the line go next?
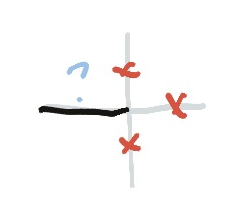
This is the dead-end situation with the ones: in that case, not all of these crosses exist until you actually draw the line, and thus eliminate the other edges of the ones.
Forbidden Corners
The line can’t split into two, so at each vertex it can only go in one of three directions. Crosses, of course, help you eliminate some of these options.
It also means that that vertex cannot be a corner on either of the squares the line approaches. Use this in conjunction with the corner ladder rule (or, I suppose, the anti-ladder rule) to eliminate the corner of another square and thus force the direction of the line over there.
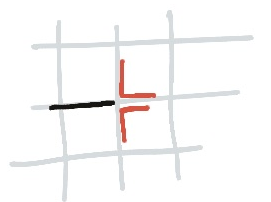
Forced Path
The opposite of a dead end is a one-way street, I suppose, so I should also mention that if you have two crosses opposite one another, then the line must go straight through that vertex, since it can’t turn.
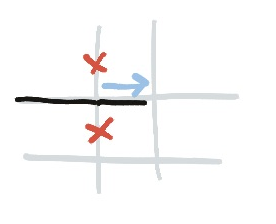
I mention this because, sometimes, you add crosses to the board and don’t notice that you’ve forced the direction of the line nearby.
This rule also works in reverse, as well: if the line continues straight, you can put crosses next to it, because the line cannot meet itself.
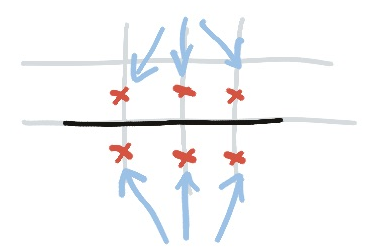
6. Ends
The line cannot break. Think about where the ends could possibly go. If you fill in or eliminate an edge, does it leave one of your ends trapped? Sometimes this is the only way to decide between options.
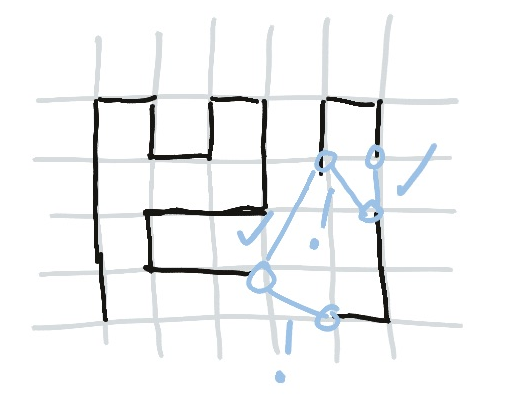
Real-life Applications
Ladders of Threes and Twos
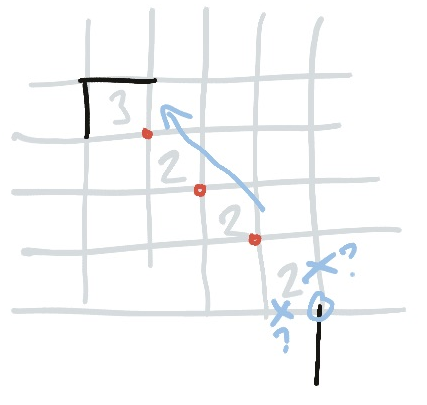
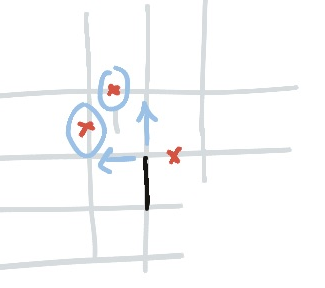
Here’s an example that shows off several rules, built on top of one another.
The S shape around the threes came from other facts on the board, but now the line approaches a cabal of twos. The line indicated by the arrow is the one we’re following.
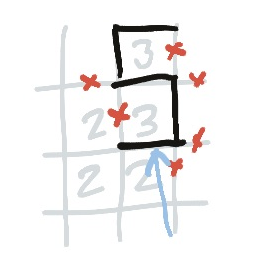
It might be obvious to you that the two that the line approaches now has two crosses on it. The upper cross came from the ladder rule of threes, and the right-hand cross came from completing the ladder2. This immediately means that the other two edges of the two must be used.
Personally, I find it harder to spot crosses like this than to spot the corner rule of twos. In fact, after I’ve filled in the juicy parts of the puzzle I tend to look for twos interacting with threes on the corners, and see if I can build a ladder based on that.
In this case, that pattern paid off in reverse. If the line were to turn downwards, this would cause a corner around a two. The corner ladder rule would thus force the next two in the chain to have the corresponding corner filled in, but there is a cross there, so it can’t. As a result, the line cannot turn downwards, and we can add a cross there.
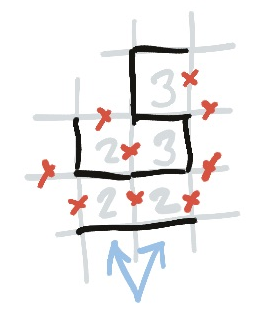
Having completed this section of the line we realise also that we have now crossed out two edges of the two that the arrow is obscuring; meaning that two also requires parallel edges. And we have crossed out a similar pattern on the other two—in the corner—so that one must also have a parallel line.
Approaching Threes: Corners Again
The above example led into this example. Forced by the requirement to have two lines around a two, we drew the horizontal line at the bottom.
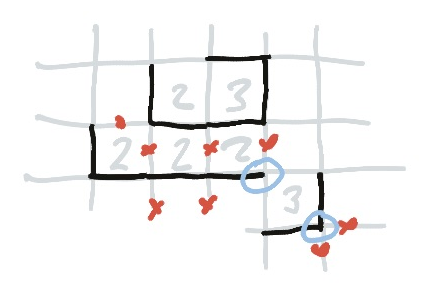
In fact, to the left was another two, whose corner was forced by the corner we drew in the previous example. This is a short corner ladder.
And to the right was another three, whose corner was also forced, but by the rule of approaching threes: one of the two edges the line meets (at the upper-left circled vertex) must be empty; thus the three is forced to use the far corner (the lower-right circled vertex).
Incidentally, I have filled in crosses below the 2-2-2 row: this was immediately relevant to me for the next part of the puzzle, but to show that would be simply to reiterate these examples.
Approaching a One
Here’s an example where we knew enough to block out two sides of a one. We don’t know which side of the three will be used, but we do know that the circled end of the line must either go straight, or turn. Both of these are edges of the same one, which means the other two edges cannot be used.
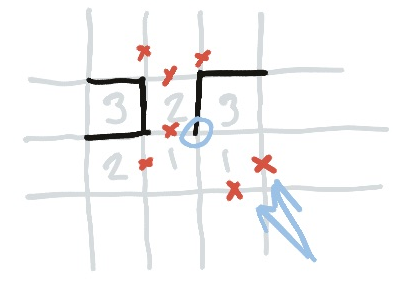
In the puzzle, this had the effect of disallowing a corner of a two, which then disallowed a chain of corners, allowing me to reason about a square not directly related to any of this!
Dead End in the Middle
In this situation we are unsure whether the line on the right will continue upwards or turn rightwards. But we have eliminated several edges in the vicinity, which is enough to see that the edge between the one and the two (indicated) cannot be used, because there are three crosses around a vertex—which means there must be a fourth.
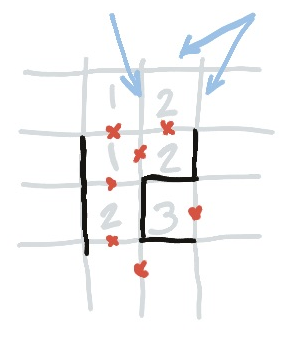
This means that the two now has two crosses by it, so the other two sides (also indicated) must be in use.
A Forbidden Corner
Here’s a situation where nothing is currently forced; all lines that can be drawn have been drawn if we only use the number of edges each square requires.
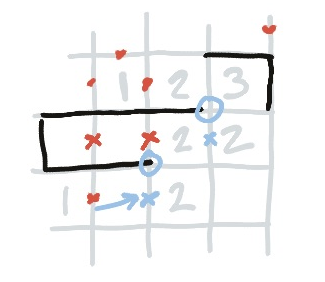
We know the line makes the shape it does because it cannot meet itself; therefore it has to stay away from itself. That explains the crosses in the middle of the diagram.
We can’t yet determine which edge of the three is the empty one, but we can extend the line at the other end. Consider the indicated edge; if we were to use it, this would force a corner ladder along the circled corners. But the upper corner is forbidden, since it would be spooning a three.
Thus we can eliminate the indicated edge, and the corresponding edge on the next corner in the ladder, and extend the line that way.
(In fact, it is enough to realise that you cannot spoon a three, and so the rightmost cross is given to us; this leaves our two with 2 crosses and 1 line: the bottom edge must also be the line.)
No Loops!
Later, we learn more about the previous example, and have enough information to guide the line around the three.
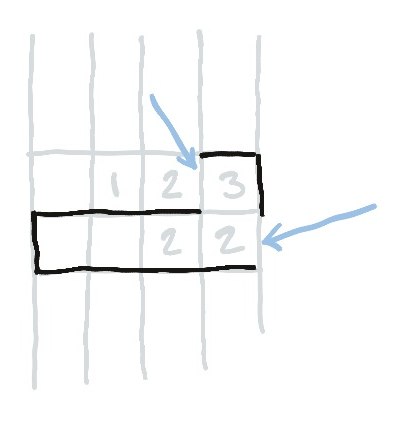
Now that we know about this extra line underneath, we can pick which edge of the three to fill in.
If we use the indicated edge (of the three), then this has the effect of forcing the other indicated edge to satisfy the two. This makes a loop, and thus is forbidden! So we know we can’t use that edge of the three.
Some for you
Here are two challenges I came across while solving puzzles myself.
In this first one, there is enough information to complete all numbered squares. Can you see the trick?

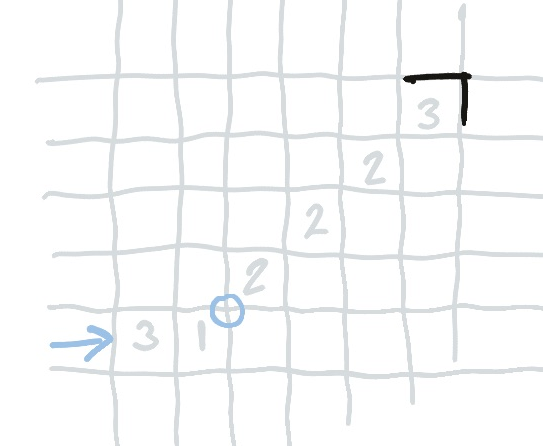
In this much larger one, there is enough information to complete the indicated three. I have circled a vertex as a clue.
That’s all
That’s all I can think of, right now. I’m sure I’ll remember some more as I do more puzzles, but the rest of the game is now applying these rules in conjunction with one another so that you can eliminate edges.
For example, sometimes you have a pattern of threes such that if you choose one edge to be open, the only path for the line is a loop. Other times, you force yourself into a dead end because you have to put too many lines around a number—or you cannot satisfy the requirements of a number.
Even knowing these rules, the puzzles are quite fiendish at the higher difficulties. They often take me an hour, with distractions. And I need distractions to reset my eyes, because sometimes I just completely miss a really obvious opportunity to apply a rule!
But sometimes, you just have to project a line and see if it breaks.
Have fun!
-
When drawing these diagrams I got a bit carried away and had failed to realise this last image is actually impossible! The reason why is left as an exercise to the reader. ↩︎
-
Eagle-eyed readers will note that I have not completed all the rules of the ladder of threes; particularly where it applies to adjacent twos. I am solving this puzzle as I write this post so that I can collect examples, and yes—I missed it! In fact, we should already have a cross below the end of the line, and another piece of line on the far side of the two! This pattern actually comes from this exact situation; the reader is invited to experiment with the same layout with the ladder around the threes reversed. ↩︎